归并排序含义及代码示例

代码示例

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;

namespace Sort
{
    class MergeSorter
    {
        /// <summary>
        /// 归并排序之归：归并排序入口 
        /// </summary>
        /// <param name="data">无序数组</param>
        /// <returns>有序数组</returns>
         public static int[] Sort(int[] data)
        {
            //若data为null，或只剩下1 or 0个元素，返回，不排序
            if (null == data || data.Length <= 1)
            {
                return data;
            }
            //取数组中间下标
            int middle = data.Length >> 1;
            //初始化临时数组let,right，并定义result作为最终有序数组，若数组元素奇数个，将把多余的那元素空间预留在right临时数组
            int[] left = new int[middle];
            int[] right =  new int[data.Length - middle];
            int[] result = new int[data.Length];
            for (int i = 0; i < data.Length; i++)
            {
                if (i < middle)
                {
                    left[i] = data[i];
                }
                else
                {
                    right[i-middle] = data[i];
                }
            }
            left = Sort(left);//递归左数组
            right = Sort(right);//递归右数组
            result = Merge(left, right);//开始排序
            return result;
        }

        /// <summary>
        /// 归并排序之并:排序在这一步
        /// </summary>
        /// <param name="a">左数组</param>
        /// <param name="b">右数组</param>
        /// <returns>合并左右数组排序后返回</returns>
         private static int[] Merge(int[] a, int[] b)
         {
            //定义结果数组，用来存储最终结果
            int[] result = new int[a.Length + b.Length];
            int i = 0, j = 0, k = 0;
            while (i < a.Length && j < b.Length)
            {
                if (a[i] < b[j])//左数组中元素小于右数组中元素
                {
                    result[k++] = a[i++];//将小的那个放到结果数组
                }
                else//左数组中元素大于右数组中元素
                {
                    result[k++] = b[j++];//将小的那个放到结果数组
                }
            }
            while (i < a.Length)//这里其实是还有左元素，但没有右元素 
            {
                result[k++] = a[i++];
            }
            while (j < b.Length)//有右元素，无左元素
            {
                result[k++] = b[j++];
            }
            return result;//返回结果数组
        }
    }
}

思想

归并（Merge）排序法是将两个（或两个以上）有序表合并成一个新的有序表，即把待排序序列分为若干个子序列，每个子序列是有序的。然后再把有序子序列合并为整体有序序列。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。

将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

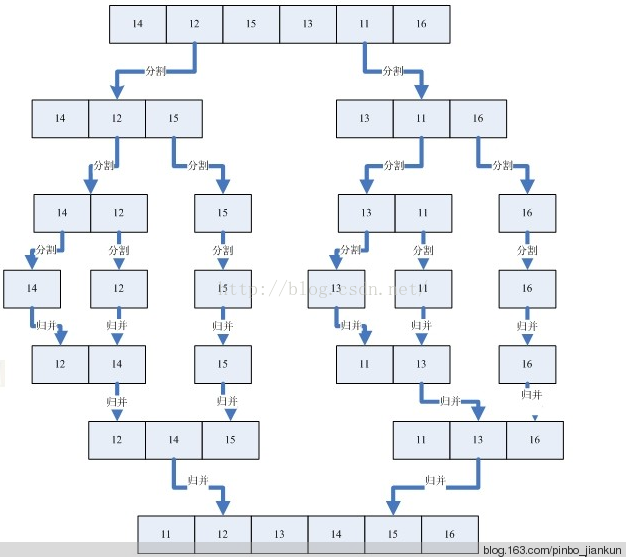
假设我们有一个没有排好序的序列，那么首先我们使用分割的办法将这个序列分割成一个一个已经排好序的子序列，然后再利用归并的方法将一个个的子序列合并成排序好的序列。分割和归并的过程可以看下面的图例。

从上图可以看出，我们首先把一个未排序的序列从中间分割成2部分，再把2部分分成4部分，依次分割下去，直到分割成一个一个的数据，再把这些数据两两归并到一起，使之有序，不停的归并，最后成为一个排好序的序列。

如何把两个已经排序好的子序列归并成一个排好序的序列呢？可以参看下面的方法。

假设我们有两个已经排序好的子序列。

序列A：1 23 34 65

序列B：2 13 14 87

那么可以按照下面的步骤将它们归并到一个序列中。

首先设定一个新的数列C[8]。
A[0]和B[0]比较，A[0] = 1，B[0] = 2，A[0] < B[0]，那么C[0] = 1
A[1]和B[0]比较，A[1] = 23，B[0] = 2，A[1] > B[0]，那么C[1] = 2
A[1]和B[1]比较，A[1] = 23，B[1] = 13，A[1] > B[1]，那么C[2] = 13
A[1]和B[2]比较，A[1] = 23，B[2] = 14，A[1] > B[2]，那么C[3] = 14
A[1]和B[3]比较，A[1] = 23，B[3] = 87，A[1] < B[3]，那么C[4] = 23
A[2]和B[3]比较，A[2] = 34，B[3] = 87，A[2] < B[3]，那么C[5] = 34
A[3]和B[3]比较，A[3] = 65，B[3] = 87，A[3] < B[3]，那么C[6] = 65
最后将B[3]复制到C中，那么C[7] = 87。归并完成。

复杂度

归并排序，时间复杂度为O(nlogn)。

归并排序的效率是比较高的，设数列长为N，将数列分开成小数列一共要logN步，每步都是一个合并有序数列的过程，时间复杂度可以记为O(N)，故一共为O(N*logN)。因为归并排序每次都是在相邻的数据中进行操作，所以归并排序在O(N*logN)的几种排序方法（快速排序，归并排序，希尔排序，堆排序）也是效率比较高的。

稳定性

稳定