最近在参与一个基于Elasticsearch作为底层数据框架提供大数据量(亿级)的实时统计查询的方案设计工作,花了些时间学习Elasticsearch的基础理论知识,整理了一下,希望能对Elasticsearch感兴趣/想了解的同学有所帮助。同时也希望有发现内容不正确或者有疑问的地方,望指明,一起探讨,学习,进步。
介绍
Elasticsearch 是一个分布式可扩展的实时搜索和分析引擎.
Elasticsearch 是一个建立在全文搜索引擎 Apache Lucene(TM) 基础上的搜索引擎.
当然 Elasticsearch 并不仅仅是 Lucene 那么简单,它不仅包括了全文搜索功能,还可以进行以下工作:
- 分布式实时文件存储,并将每一个字段都编入索引,使其可以被搜索。
- 实时分析的分布式搜索引擎。
- 可以扩展到上百台服务器,处理PB级别的结构化或非结构化数据。
基本概念
先说Elasticsearch的文件存储,Elasticsearch是面向文档型数据库,一条数据在这里就是一个文档,用JSON作为文档序列化的格式,比如下面这条用户数据:
1 | { |
用MySQL这样的数据库存储就会容易想到建立一张User表,有balabala的字段等,在Elasticsearch里这就是一个文档,当然这个文档会属于一个User的类型,各种各样的类型存在于一个索引当中。这里有一份简易的将Elasticsearch和关系型数据术语对照表:
关系数据库 ⇒ 数据库 ⇒ 表 ⇒ 行 ⇒ 列(Columns)
Elasticsearch ⇒ 索引 ⇒ 类型 ⇒ 文档 ⇒ 字段(Fields)
一个 Elasticsearch 集群可以包含多个索引(数据库),也就是说其中包含了很多类型(表)。这些类型中包含了很多的文档(行),然后每个文档中又包含了很多的字段(列)。
Elasticsearch的交互,可以使用Java API,也可以直接使用HTTP的Restful API方式,比如我们打算插入一条记录,可以简单发送一个HTTP的请求:
1 | PUT /megacorp/employee/1 |
更新,查询也是类似这样的操作,具体操作手册可以参见Elasticsearch权威指南
索引
Elasticsearch最关键的就是提供强大的索引能力了,其实InfoQ的这篇时间序列数据库的秘密(2)——索引写的非常好,我这里也是围绕这篇结合自己的理解进一步梳理下,也希望可以帮助大家更好的理解这篇文章。
Elasticsearch索引的精髓:
一切设计都是为了提高搜索的性能
另一层意思:为了提高搜索的性能,难免会牺牲某些其他方面,比如插入/更新,否则其他数据库不用混了:)
前面看到往Elasticsearch里插入一条记录,其实就是直接PUT一个json的对象,这个对象有多个fields,比如上面例子中的name, sex, age, about, interests,那么在插入这些数据到Elasticsearch的同时,Elasticsearch还默默的为这些字段建立索引–倒排索引,因为Elasticsearch最核心功能是搜索。
Elasticsearch默认会为每个字段根据value的类型分别建立索引,如果不想为某些字段建立索引或者不做分词分析的话,需要通过FieldMapping注明。
Elasticsearch是如何做到快速索引的
InfoQ那篇文章里说Elasticsearch使用的倒排索引比关系型数据库的B-Tree索引快,为什么呢?
什么是B-Tree索引?
上大学读书时老师教过我们,二叉树查找效率是logN,同时插入新的节点不必移动全部节点,所以用树型结构存储索引,能同时兼顾插入和查询的性能。
因此在这个基础上,再结合磁盘的读取特性(顺序读/随机读),传统关系型数据库采用了B-Tree/B+Tree这样的数据结构:
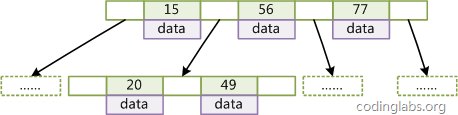
为了提高查询的效率,减少磁盘寻道次数,将多个值作为一个数组通过连续区间存放,一次寻道读取多个数据,同时也降低树的高度。
什么是倒排索引?

继续上面的例子,假设有这么几条数据(为了简单,去掉about, interests这两个field):
| ID | Name | Age | Sex |
|---|---|---|---|
| 1 | Kate | 24 | Female |
| 2 | John | 24 | Male |
| 3 | Bill | 29 | Male |
ID是Elasticsearch自建的文档id,那么Elasticsearch建立的索引如下:
Name:
| Term | Posting List |
|---|---|
| Kate | 1 |
| John | 2 |
| Bill | 3 |
Age:
| Term | Posting List |
|---|---|
| 24 | [1,2] |
| 29 | 3 |
Sex:
| Term | Posting List |
|---|---|
| Female | 1 |
| Male | [2,3] |
Posting List
Elasticsearch分别为每个field都建立了一个倒排索引,Kate, John, 24, Female这些叫term,而[1,2]就是Posting List。Posting list就是一个int的数组,存储了所有符合某个term的文档id。
看到这里,不要认为就结束了,精彩的部分才刚开始…
通过posting list这种索引方式似乎可以很快进行查找,比如要找age=24的同学,爱回答问题的小明马上就举手回答:我知道,id是1,2的同学。但是,如果这里有上千万的记录呢?如果是想通过name来查找呢?
Term Dictionary
Elasticsearch为了能快速找到某个term,将所有的term排个序,二分法查找term,logN的查找效率,就像通过字典查找一样,这就是Term Dictionary。现在再看起来,似乎和传统数据库通过B-Tree的方式类似啊,为什么说比B-Tree的查询快呢?
Term Index
B-Tree通过减少磁盘寻道次数来提高查询性能,Elasticsearch也是采用同样的思路,直接通过内存查找term,不读磁盘,但是如果term太多,term dictionary也会很大,放内存不现实,于是有了Term Index,就像字典里的索引页一样,A开头的有哪些term,分别在哪页,可以理解term index是一颗树: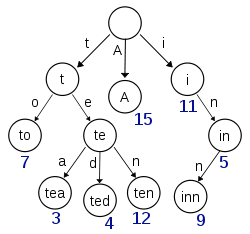
这棵树不会包含所有的term,它包含的是term的一些前缀。通过term index可以快速地定位到term dictionary的某个offset,然后从这个位置再往后顺序查找。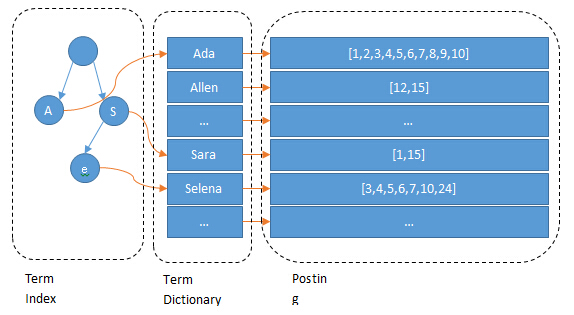
所以term index不需要存下所有的term,而仅仅是他们的一些前缀与Term Dictionary的block之间的映射关系,再结合FST(Finite State Transducers)的压缩技术,可以使term index缓存到内存中。从term index查到对应的term dictionary的block位置之后,再去磁盘上找term,大大减少了磁盘随机读的次数。
这时候爱提问的小明又举手了:”那个FST是神马东东啊?”
一看就知道小明是一个上大学读书的时候跟我一样不认真听课的孩子,数据结构老师一定讲过什么是FST。但没办法,我也忘了,这里再补下课:
FSTs are finite-state machines that map a term (byte sequence) to an arbitrary output.
假设我们现在要将mop, moth, pop, star, stop and top(term index里的term前缀)映射到序号:0,1,2,3,4,5(term dictionary的block位置)。最简单的做法就是定义个Map<String, Integer>,大家找到自己的位置对应入座就好了,但从内存占用少的角度想想,有没有更优的办法呢?答案就是:FST(理论依据在此,但我相信99%的人不会认真看完的)
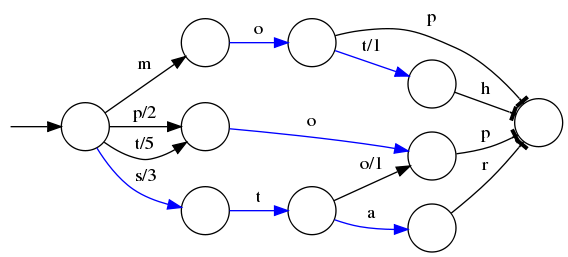
⭕️表示一种状态
–>表示状态的变化过程,上面的字母/数字表示状态变化和权重
将单词分成单个字母通过⭕️和–>表示出来,0权重不显示。如果⭕️后面出现分支,就标记权重,最后整条路径上的权重加起来就是这个单词对应的序号。
FSTs are finite-state machines that map a term (byte sequence) to an arbitrary output.
FST以字节的方式存储所有的term,这种压缩方式可以有效的缩减存储空间,使得term index足以放进内存,但这种方式也会导致查找时需要更多的CPU资源。
后面的更精彩,看累了的同学可以喝杯咖啡……
http://examples.mikemccandless.com/fst.py
Amazon DynamoDB
Cassandra
Elasticsearch
Hive
MongoDB
MySQL
PostgreSQL
SQLite
压缩技巧
Elasticsearch里除了上面说到用FST压缩term index外,对posting list也有压缩技巧。
小明喝完咖啡又举手了:”posting list不是已经只存储文档id了吗?还需要压缩?”
嗯,我们再看回最开始的例子,如果Elasticsearch需要对同学的性别进行索引(这时传统关系型数据库已经哭晕在厕所……),会怎样?如果有上千万个同学,而世界上只有男/女这样两个性别,每个posting list都会有至少百万个文档id。
Elasticsearch是如何有效的对这些文档id压缩的呢?
Frame Of Reference
增量编码压缩,将大数变小数,按字节存储
首先,Elasticsearch要求posting list是有序的(为了提高搜索的性能,再任性的要求也得满足),这样做的一个好处是方便压缩,看下面这个图例: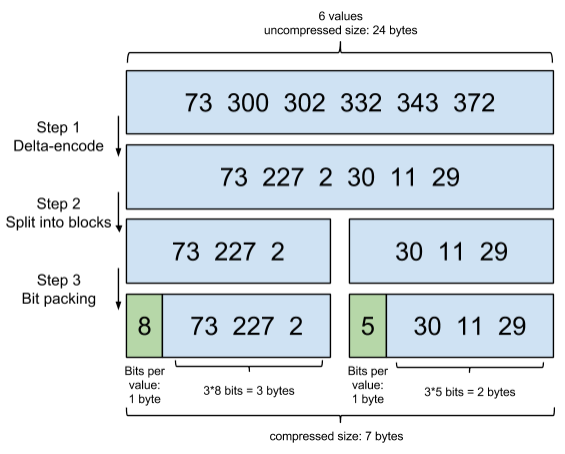
如果数学不是体育老师教的话,还是比较容易看出来这种压缩技巧的。
原理就是通过增量,将原来的大数变成小数仅存储增量值,再精打细算按bit排好队,最后通过字节存储,而不是大大咧咧的尽管是2也是用int(4个字节)来存储。
Roaring bitmaps
说到Roaring bitmaps,就必须先从bitmap说起。Bitmap是一种数据结构,假设有某个posting list:
[1,3,4,7,10]
对应的bitmap就是:
[1,0,1,1,0,0,1,0,0,1]
非常直观,用0/1表示某个值是否存在,比如10这个值就对应第10位,对应的bit值是1,这样用一个字节就可以代表8个文档id,旧版本(5.0之前)的Lucene就是用这样的方式来压缩的,但这样的压缩方式仍然不够高效,如果有1亿个文档,那么需要12.5MB的存储空间,这仅仅是对应一个索引字段(我们往往会有很多个索引字段)。于是有人想出了Roaring bitmaps这样更高效的数据结构。
Bitmap的缺点是存储空间随着文档个数线性增长,Roaring bitmaps需要打破这个魔咒就一定要用到某些指数特性:
将posting list按照65535为界限分块,比如第一块所包含的文档id范围在0 ~ 65535之间,第二块的id范围是65536 ~ 131071,以此类推。再用<商,余数>的组合表示每一组id,这样每组里的id范围都在0 ~ 65535内了,剩下的就好办了,既然每组id不会变得无限大,那么我们就可以通过最有效的方式对这里的id存储。
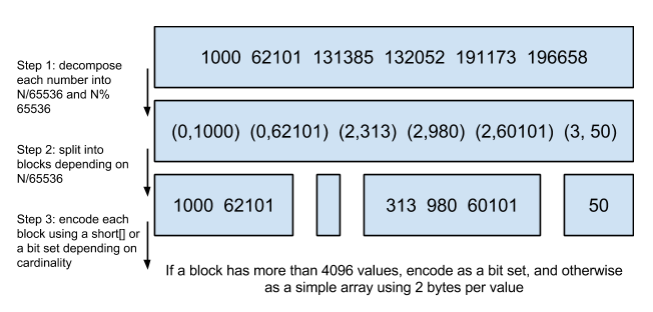
细心的小明这时候又举手了:”为什么是以65535为界限?”
程序员的世界里除了1024外,65535也是一个经典值,因为它=2^16-1,正好是用2个字节能表示的最大数,一个short的存储单位,注意到上图里的最后一行“If a block has more than 4096 values, encode as a bit set, and otherwise as a simple array using 2 bytes per value”,如果是大块,用节省点用bitset存,小块就豪爽点,2个字节我也不计较了,用一个short[]存着方便。
那为什么用4096来区分采用数组还是bitmap的阀值呢?
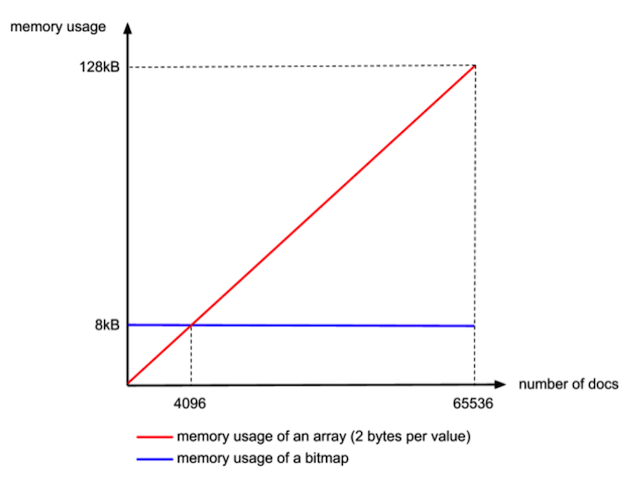
这个是从内存大小考虑的,当block块里元素超过4096后,用bitmap更省空间:
采用bitmap需要的空间是恒定的: 65536/8 = 8192bytes
而如果采用short[],所需的空间是: 2*N(N为数组元素个数)
小明手指一掐N=4096刚好是边界:
联合索引
上面说了半天都是单field索引,如果多个field索引的联合查询,倒排索引如何满足快速查询的要求呢?
- 利用跳表(Skip list)的数据结构快速做“与”运算,或者
- 利用上面提到的bitset按位“与”
先看看跳表的数据结构:
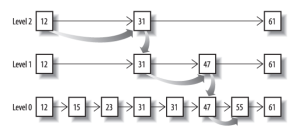
将一个有序链表level0,挑出其中几个元素到level1及level2,每个level越往上,选出来的指针元素越少,查找时依次从高level往低查找,比如55,先找到level2的31,再找到level1的47,最后找到55,一共3次查找,查找效率和2叉树的效率相当,但也是用了一定的空间冗余来换取的。
假设有下面三个posting list需要联合索引:
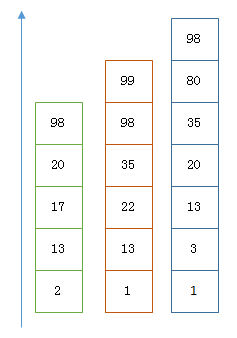
如果使用跳表,对最短的posting list中的每个id,逐个在另外两个posting list中查找看是否存在,最后得到交集的结果。
如果使用bitset,就很直观了,直接按位与,得到的结果就是最后的交集。
总结和思考
Elasticsearch的索引思路:
将磁盘里的东西尽量搬进内存,减少磁盘随机读取次数(同时也利用磁盘顺序读特性),结合各种奇技淫巧的压缩算法,用及其苛刻的态度使用内存。
所以,对于使用Elasticsearch进行索引时需要注意:
- 不需要索引的字段,一定要明确定义出来,因为默认是自动建索引的
- 同样的道理,对于String类型的字段,不需要analysis的也需要明确定义出来,因为默认也是会analysis的
- 选择有规律的ID很重要,随机性太大的ID(比如java的UUID)不利于查询
看一下filebeat收集日志后,elasticsearch自动生成的id,如图: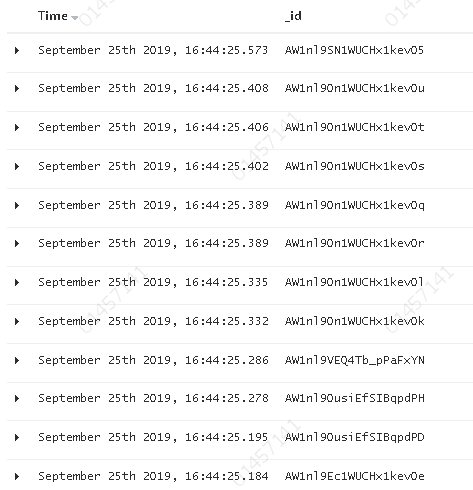
关于最后一点,个人认为有多个因素:
其中一个(也许不是最重要的)因素: 上面看到的压缩算法,都是对Posting list里的大量ID进行压缩的,那如果ID是顺序的,或者是有公共前缀等具有一定规律性的ID,压缩比会比较高;
另外一个因素: 可能是最影响查询性能的,应该是最后通过Posting list里的ID到磁盘中查找Document信息的那步,因为Elasticsearch是分Segment存储的,根据ID这个大范围的Term定位到Segment的效率直接影响了最后查询的性能,如果ID是有规律的,可以快速跳过不包含该ID的Segment,从而减少不必要的磁盘读次数,具体可以参考这篇如何选择一个高效的全局ID方案(评论也很精彩)
后续再结合实际开发及调优工作分享更多内容,敬请期待!
拓展
倒排索引:ES倒排索引底层原理及FST算法的实现过程
字典树:Trie(Prefix Tree)原理
一直以来,数据结构的“小”而“快”是每个追求更好性能的developer孜孜不倦追求的目标,所谓“快”即检索速度快,“小”即通用最小化算法。上一节我们介绍了倒排表的数据压缩原理和过程,自本节开始,我们分几部分详细介绍一下Lucene中对倒排索引Term DIctionary以及Term Index的数据压缩和优化算法。
我们已经了解到,Term Dictionary是字典序非重复的 K-V 结构的,而通常搜索引擎级别的倒排索引,Term Dictionary 动辄以“亿”起步,这势必要求我们在做数据存储时对其数据结构有极其高的要求。以图4-1为例,假设途中英汉词典片段就是我们要存储的词项字典,为了遵循“通用最小化算法”对其进行数据压缩,我们就必须要考虑如何以最小的代价换区最高的效率。通过观察不难发现,无论任何一个Term,无外乎由26个英文字母组成,这也就意味越多的词项就会造成的越多的数据“重复”。这里所说的重复指的是词项之间会有很多个公共部分,如“abandon”和“abandonment”就共享了公共前缀“abandonment”。我们是否可以像Java开发过程中对代码的封装那样,重复利用这一部分公共内容呢?答案是肯定的!Lucene在存储这种有重复字符的数据的时候,只会存储一次,也就是哪怕有一亿个以abandon为前缀的词项,“abandom”这个前缀也只会存储一次。这里就用到了一种我们经常用到的一种数据结构:Trie即字典树,也叫前缀树(Prefix Tree)。下面我们以Term Dictionary:(msb、msbtech、msn、wltech)为例,演示一下Trie是如何存储Term Dictionary的。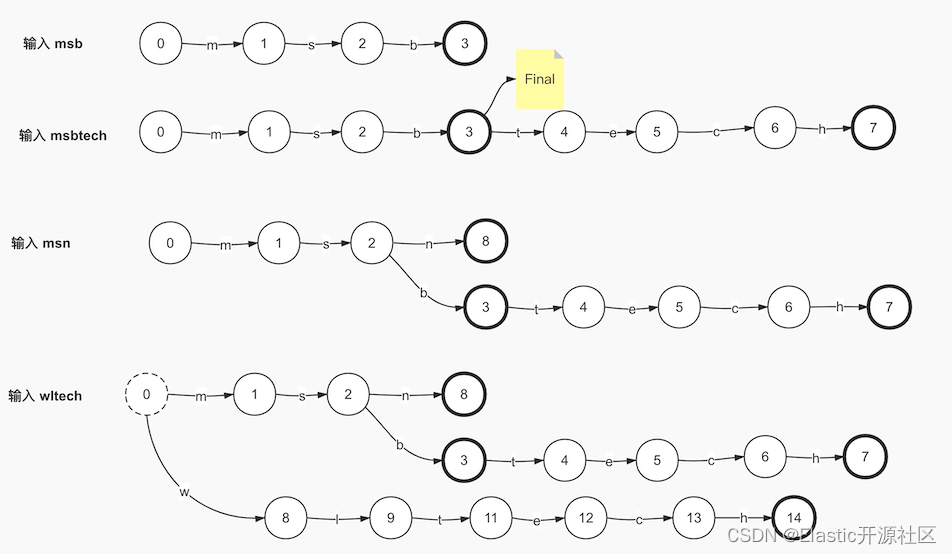
如上图4-2所示,我们按照每个Term一步来演示Trie是如何存储Term Dictionary的。图中我们以圆形标识节点,箭头代表节点的出度,出度存储了当前节点对应的字符。当输入词项“msb”的时候,如果图中第一步所示,图中以加粗的圆圈标识当前节点是一个终止节点。当输入第二个词项“msbtech”的时候,复用了“msb”,当输入“msn”的时候,节点2添加了第二个出度,至此我们已经实现了对重复关键字的复用。但是问题也就随之而来了,当最后一个Term输入的时候,节点0产生了第二个出度。
FST的构建原理
细心的你应该已经发现了,在使用字典树存储Term Dictionary的案例中,字符“tech”也属于重复部分,但是未被合理复用,导致了空间浪费。为了解决这个问题,Lucene采用了另一种数据结构:FST(Finite State Transducer),即“有限状态转换机”。FST是本章内容难点,也是倒排索引的核心数据结构。
通常我们在计算机的语言中标示一件事物,都会通过某种数学模型来描述。假如现在我们要描述一件事:张三一天的所有活动。这里我们采用了一种叫做FSM(Finite State Machine)的抽象模型,如图5-1所示,这种模型使用原型的节点标示某个“状态”,状态之间可以互相转换,但是转换过程是无向的。比如睡觉醒了可以去工作,工作累了可以去玩手机;或者工作中想去上厕所等等。在这个模型中,标示状态的节点是有限多个的,但状态的转换的情况是无限多的,同一时刻只能处于某一个状态,并且状态的转换是无序切循环的。
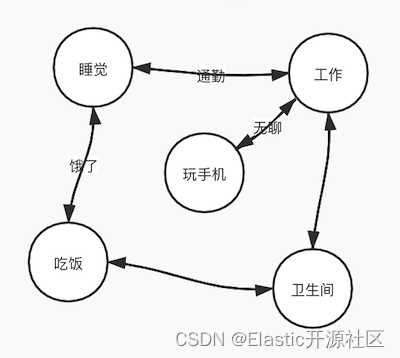
显然这种模型并不适用于描述Term Dictionary这样的数据结构,但是我们之所以提他,是为了方便读者理解这种具化事务抽象化描述的方式。虽然FSM并不适合,但是在他的基础上演化出了FSA(Finite State Acceptor),我们仍然以图 4-2 中的Term Dictionary数据为例,演示一下FSA是如何在Trie的基础上进行优化的。
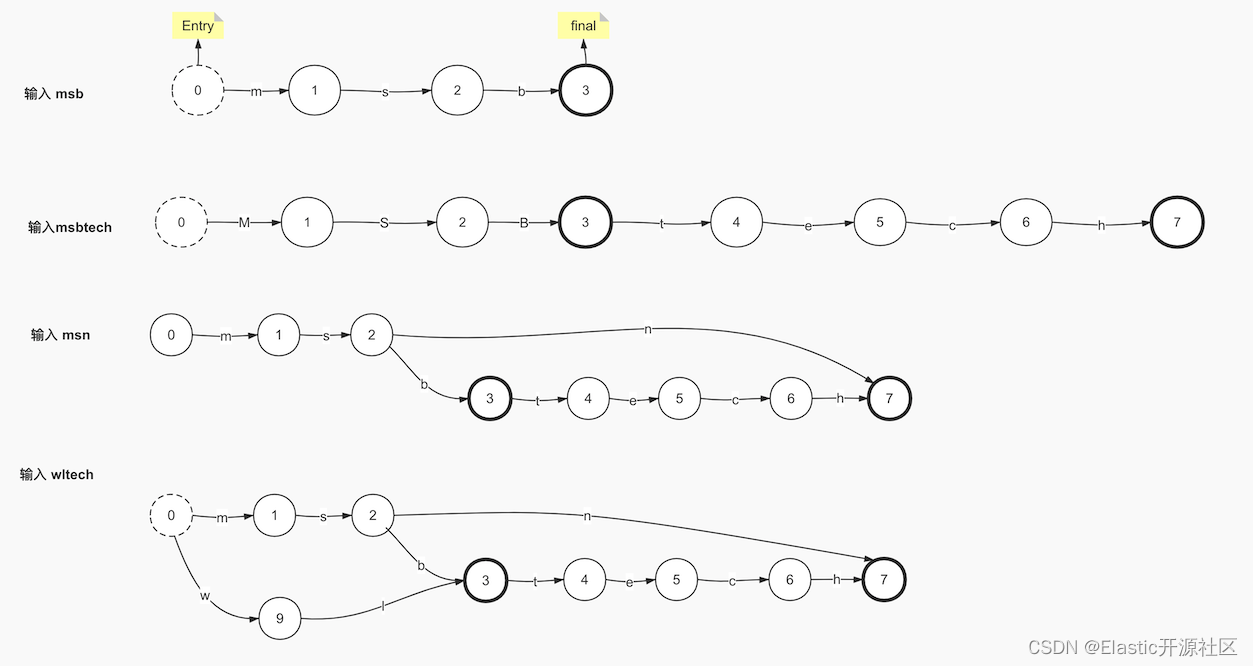
如上图5-2所示,相较于FSM,FSA增加了Entry和Final的概念,也就是由状态转换的不确定性变为了确定,由闭环变为了单向有序,这一点和Trie是类似的,但是不同的是,FSA的Final节点是唯一的,也是因为这个原因,FSA在录入和Trie相同的Term Dictionary数据的时候,从第三步开始才表现出了区别,即尾部复用。如果在第三步的时候还不太明显,那第四步中就可以清楚的看到FSA在后缀的处理上更加高效。
至此,FSA已经满足了对Term Dictionary数据高效存储的基本要求,但是仍然不满足的一个问题就是,FSA无法存储key-value的数据类型,所以FST在此基础上为每一个出度添加了一个output属性,用来表示每个term的value值。下面以Term Dictionary:(msb/10、msbtech/5、msn/2、wltech/8、wth/16)为例,演示一下FST的构建原理,斜线后面的数字代表每个term的输出值。

通用最小化算法的应用面非常广泛,这里其实也是遵循了这样的规则。可复用的不仅仅Term的字符,输出值之所以被存储了最靠前的位置上,目的也是为了让更多的Term复用,如果输出值产生了冲突,再去处理冲突问题,最终生成最小化FST。
如上图5-3所示,当第一个term:msb被写入FST中,其输出值被保存在了其第一个节点的出度上,在数据从FST中读取的时候, 计算其每个节点对应的出度的输出值以及终止节点的final output值的累加和,从而得出输出值,此时msb的输出值就是10+0+0+0=10,但是这里我用0来标识没有输出值,但实际情况没有输出值就是空而不是0,这里写0只是为了方便你去理解,这一点是需要注意的。
当第二个term:msbteach被写入的时候,其输出值5与msb的输出值10发生了冲突,这时,通用最小化算法法则再次发挥了功效。数字虽然不能像字符那样以前缀作为复用手段,但是数字是可以累加的,10可以拆成两个数字5,这样10和5就产生了公共部分,即5,所以这个时候m的输出值就需要改成5,那另一个5就需要找一个合适的位置,然而把它存放在任何一个节点的出度上似乎都会影响msbtech的计算结果,为了避免这个问题,可以把这个多出来的属于msb的输出值存入msb的final节点的final output中,节点的final output只会在当前出度是输入值的最后一个字符并且出度的target指向的是final节点的时候,才会参与计算。因此此时的msb和msbtech就各自把输出值存入了合适的位置,互不影响而且做到了“通用最小化”原则。
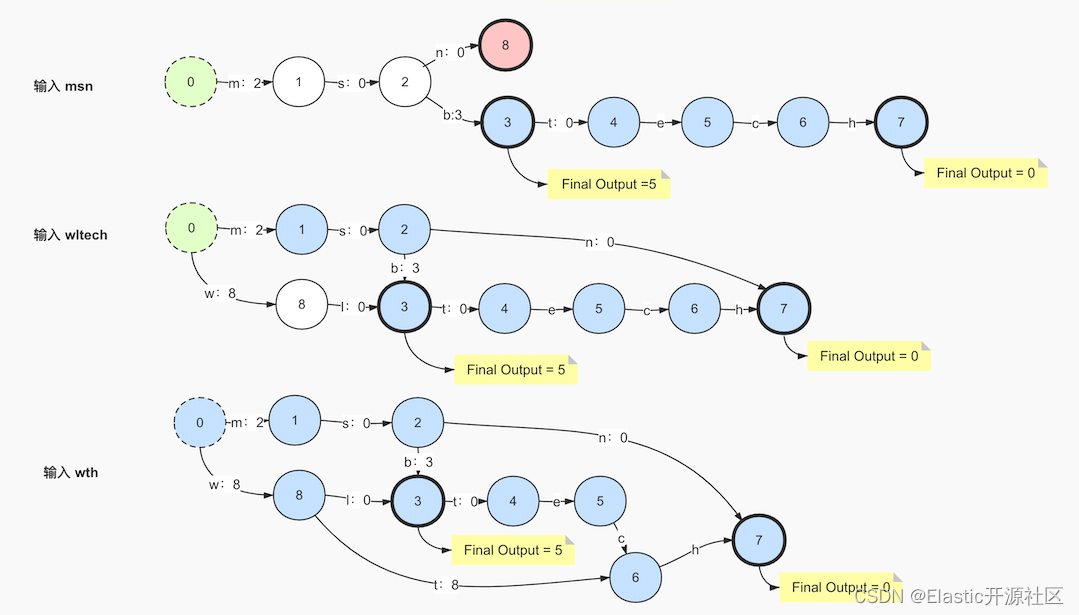
输入第三个term:msn,节点2产生了第二个出度:n,2 < 5,根据”通用最小化”法则,2和5有公共部分:2,5倍拆分成了2和3,此时公共前缀为“ms”,前面以“ms”为前缀的所有term都讲重新计算出度output,此时3需要满足:不能存放在公共前缀“ms”上,并且也不能在第二条出度“n”上,因此只能存放在出度b上,因为b在当前节点2第一条出度的链路上是最靠前的位置。这里FST和Trie最大的区别就是FST不仅使用了公共前缀,而且还计算了公共后缀,“msn”的最终节点会指向节点7,和节点6的出度h共享终止节点。
其实到这里还不能很好的提现“公共后缀”,但是输入wltech的时候,此时就产生了公共后缀“tech”,节点2的出度b和节点8的出度t共同指向了节点3。
输入最后一个term:wth,公共前缀为w,公共后缀为h,最终生成的FST如上图5-4所示。
为什么Elasticsearch比MySQL的检索快?
对比MySQL的B+Tree索引原理,可以发现:
Lucene的Term index和Term Dictionary其实对应的就是MySQL的B+Tree的功能,为关键字key提供索引。Lucene的inverted index可以比MySQL的b-tree检索更快。Term index在内存中是以FST(finite state transducers)的形式保存的,其特点是非常节省内存。所以Lucene搜索一个关键字key的速度是非常快的,而MySQL的B+Tree需要读磁盘比较。Term dictionary在磁盘上是以分block的方式保存的,一个block内部利用公共前缀压缩,比如都是Ab开头的单词就可以把Ab省去。这样Term dictionary可以比B-tree更节约磁盘空间。Lucene对不同的数据类型采用了不同的索引方式,上面分析是针对field为字符串的,比如针对int,有TrieIntField类型,针对经纬度,就可以用GeoHash编码。在 MySQL中给两个字段独立建立的索引无法联合起来使用,必须对联合查询的场景建立复合索引,而Lucene可以任何AND或者OR组合使用索引进行检索。
倒排检索加速_工业界如何利用跳表、哈希表、位图进行加速?
这里其实就是多字段检索比MySQL快的原因;
es通过FST找到倒排索引的位置获取文档id列表,再通过跳表等来快速合并文档列表。
其实FST、跳表合并这些都是Lucene实现的

